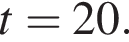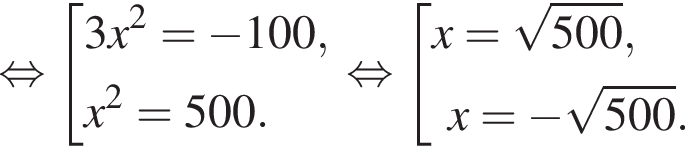Даны дроби 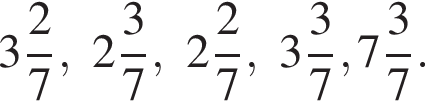 Укажите дробь, которая равна дроби
Укажите дробь, которая равна дроби ![]()
На рисунке изображен треугольник ABC, в котором ∠ACB = 38°, ∠AMN = 109°. Используя данные рисунка, найдите градусную меру угла BAC.
Среди точек
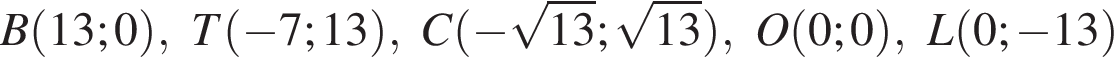 выберите ту, которая принадлежит графику функции, изображённому на рисунке:
выберите ту, которая принадлежит графику функции, изображённому на рисунке:
Если 15% некоторого числа равны 33, то 20% этого числа равны:
Одно число меньше другого на 75, что составляет 15% большего числа. Найдите меньшее число.
Результат упрощения выражения 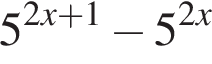 имеет вид:
имеет вид:
Решите неравенство 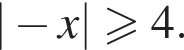
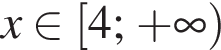
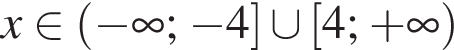
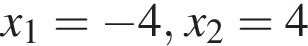

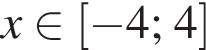
От листа жести, имеющего форму квадрата, отрезали прямоугольную полосу шириной 7 дм, после чего площадь оставшейся части листа оказалась равной 30 дм2. Длина стороны квадратного листа (в дециметрах) была равна:
Одна из сторон прямоугольника на 7 см длиннее другой, а его площадь равна 78 см2. Уравнение, одним из корней которого является длина меньшей стороны прямоугольника, имеет вид:
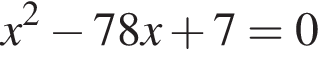 ;
;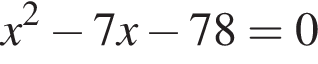 ;
;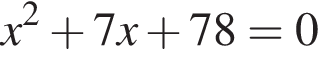 ;
;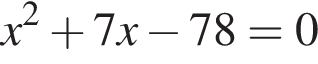 ;
;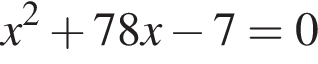 .
.Прямая a пересекает плоскость α в точке A и образует с плоскостью угол 60°. Точка B лежит на прямой a, причем AB = ![]() Найдите расстояние от точки B до плоскости α.
Найдите расстояние от точки B до плоскости α.
Даны два числа. Известно, что одно из них меньше другого на 6. Какому условию удовлетворяет меньшее число x, если его удвоенный квадрат не больше суммы квадратов этих чисел?

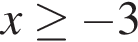

Упростите выражение 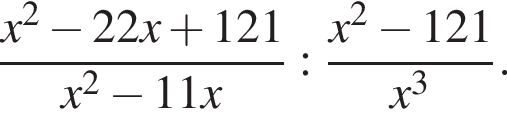
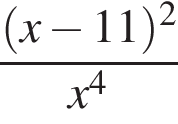
Параллельно стороне треугольника, равной 12, проведена прямая. Длина отрезка этой прямой, заключенного между сторонами треугольника, равна 8. Найдите отношение площади полученной трапеции к площади исходного треугольника.
Сумма координат точки пересечения прямых, заданных уравнениями 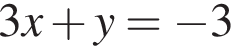 и
и 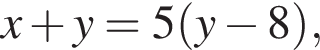 равна:
равна:
Количество целых решений неравенства 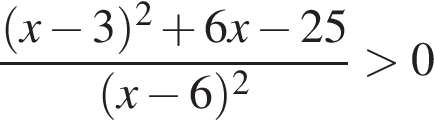 на промежутке
на промежутке  равно:
равно:
Из полного бокала, имеющего форму конуса высотой 9, отлили треть (по объему) жидкости. Вычислите ![]() где h — высота оставшейся жидкости.
где h — высота оставшейся жидкости.
Через вершину A прямоугольного треугольника ABC (∠C = 90°) проведен перпендикуляр AK к его плоскости. Найдите расстояние от точки K до прямой BC, если AK = 4, AB = 9, BC = ![]()
Найдите наименьший положительный корень уравнения 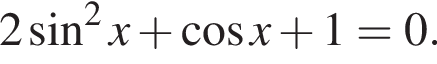
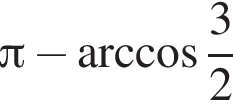
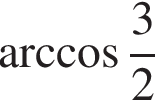
Автомобиль проехал некоторое расстояние, израсходовав 21 л топлива. Расход топлива при этом составил 9 л на 100 км пробега. Затем автомобиль существенно увеличил скорость, в результате чего расход топлива вырос до 12 л на 100 км. Сколько литров топлива понадобится автомобилю, чтобы проехать такое же расстояние?
Найдите произведение большего корня на количество корней уравнения 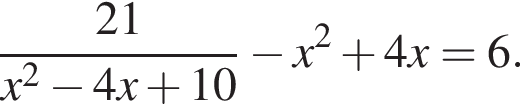
Основание остроугольного равнобедренного треугольника равно 4, а синус противоположного основанию угла равен 0,6. Найдите площадь треугольника.
Пусть (x; y) — решение системы уравнений 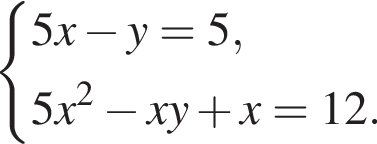
Найдите значение 5y − x.
Найдите сумму (в градусах) наименьшего положительного и наибольшего отрицательного корней уравнения 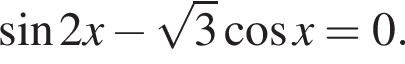
Найдите количество корней уравнения  на промежутке
на промежутке 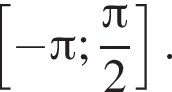
Решите уравнение 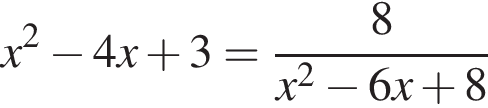 и найдите сумму его корней.
и найдите сумму его корней.
Найдите значение выражения: 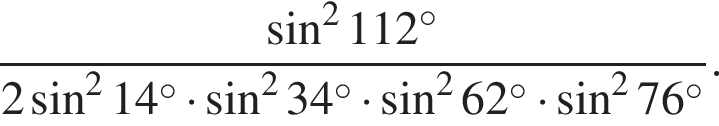
Найдите сумму целых значений x, принадлежащих области определения функции
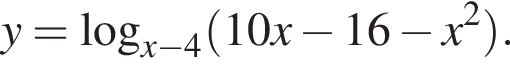
Прямоугольный треугольник с катетами, равными ![]() и
и ![]() вращается вокруг оси, содержащей его гипотенузу. Найдите значение выражения
вращается вокруг оси, содержащей его гипотенузу. Найдите значение выражения ![]() где V — объём фигуры вращения.
где V — объём фигуры вращения.
Если 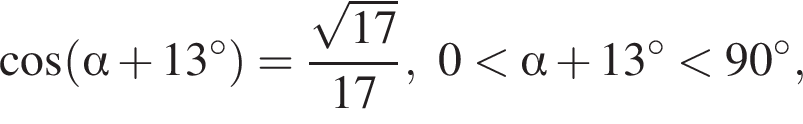 то значение выражения
то значение выражения 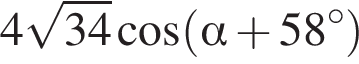 равно ...
равно ...
Найдите произведение корней уравнения 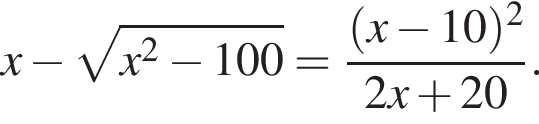

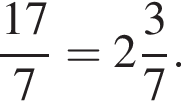
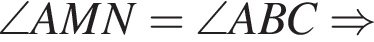
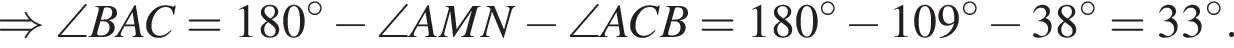
 представляет собой прямую, проходящую через точки вида
представляет собой прямую, проходящую через точки вида 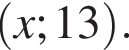 Таким образом, единственное подходящее решение — точка T.
Таким образом, единственное подходящее решение — точка T.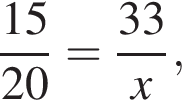 где x — неизвестное число.
где x — неизвестное число.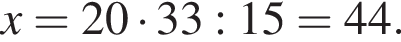
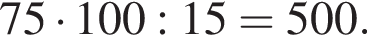 Таким образом, меньшее число
Таким образом, меньшее число 
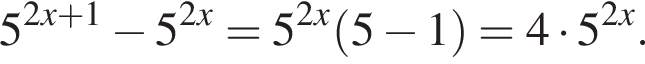

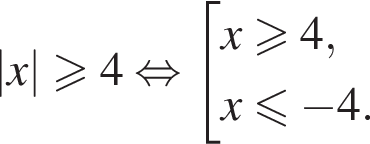
 Тогда:
Тогда: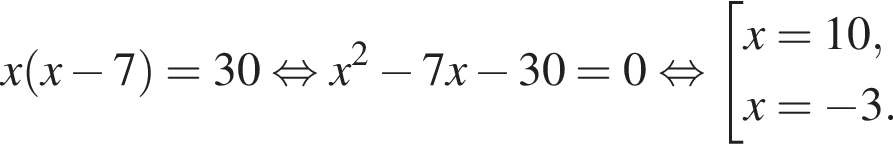
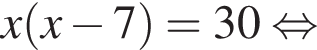
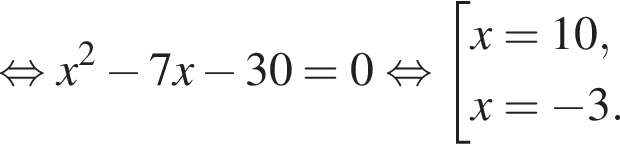
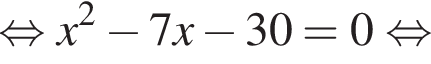
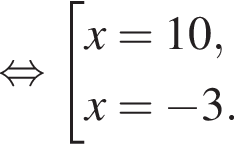
 Тогда получаем:
Тогда получаем: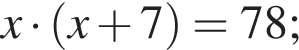
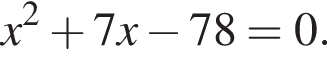

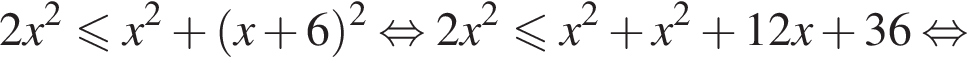

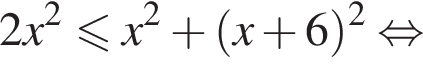
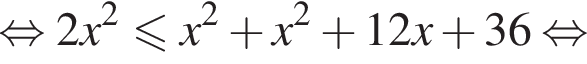
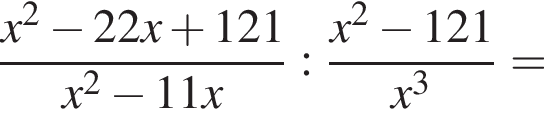
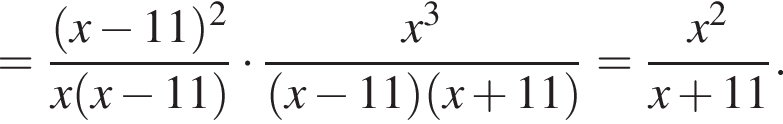
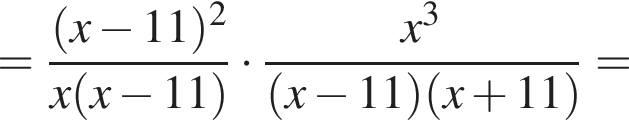
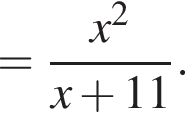
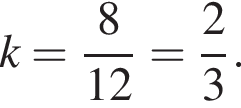 Площади подобных фигур относятся как квадрат коэффициента подобия. Поэтому
Площади подобных фигур относятся как квадрат коэффициента подобия. Поэтому 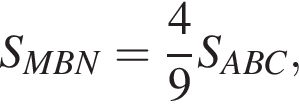 а тогда
а тогда 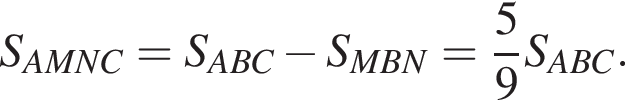
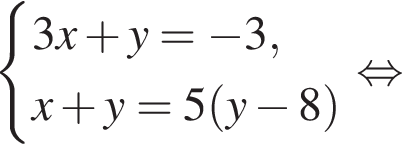
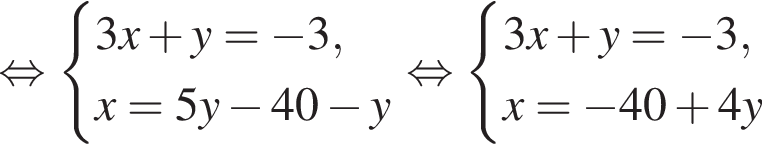
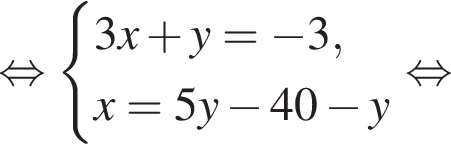
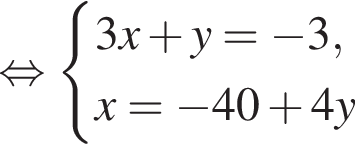
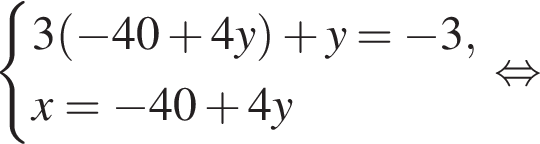
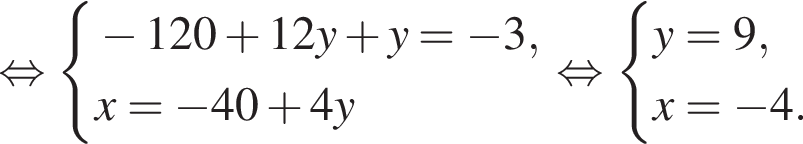
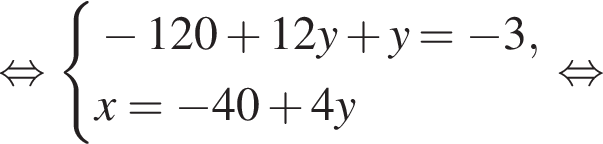
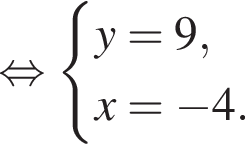
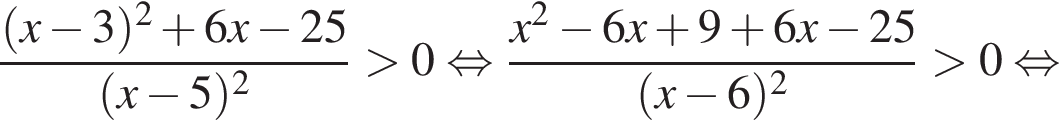
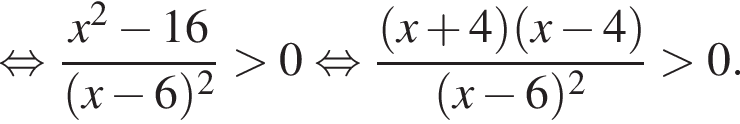
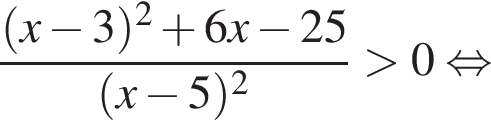
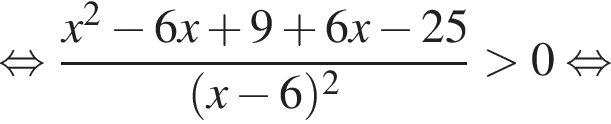
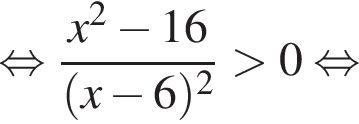
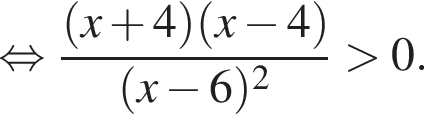
 Корни знаменателя
Корни знаменателя  Следовательно, существует только 3 целых решения.
Следовательно, существует только 3 целых решения. 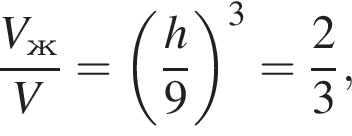 откуда
откуда 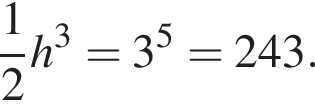
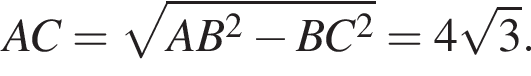 Заметим, что AC является проекцией наклонной KC на плоскость ABC и AC
Заметим, что AC является проекцией наклонной KC на плоскость ABC и AC
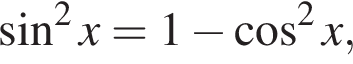 получим:
получим: 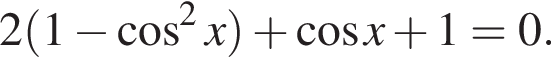 Сделаем замену
Сделаем замену 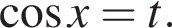 Решим уравнение:
Решим уравнение:
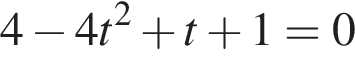
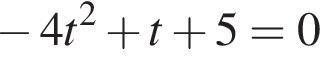
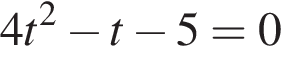
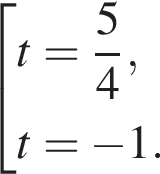
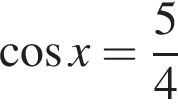 или
или 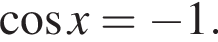 Первое уравнение решений не имеет, поскольку
Первое уравнение решений не имеет, поскольку 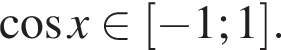 Рассмотрим второе уравнение:
Рассмотрим второе уравнение: 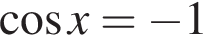
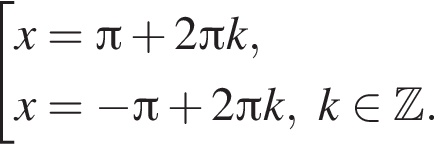
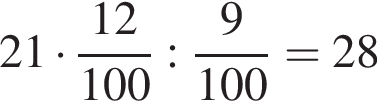 л.
л.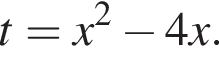 Тогда:
Тогда: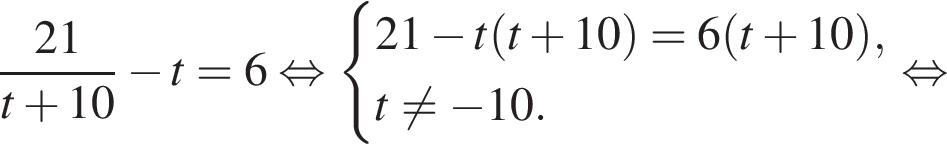
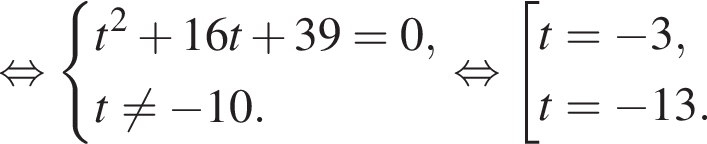
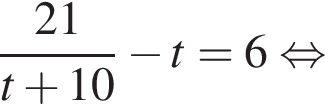
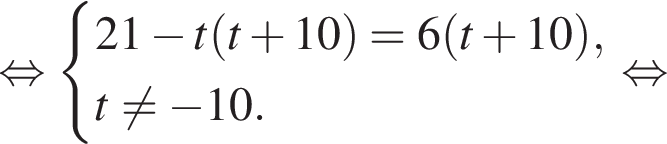
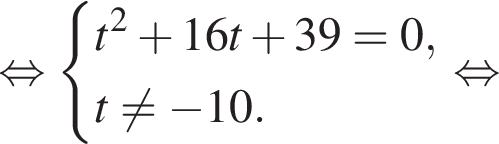
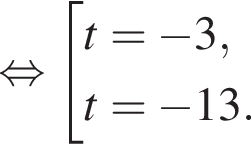
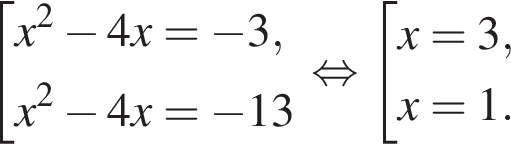
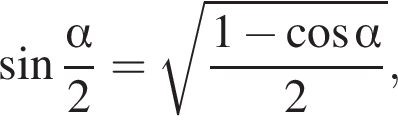 где
где 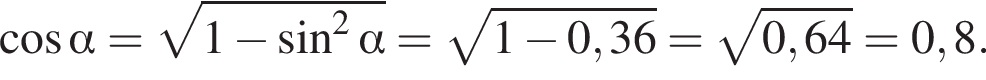
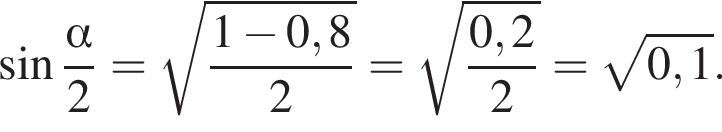
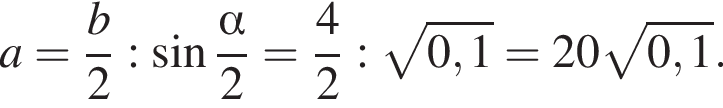
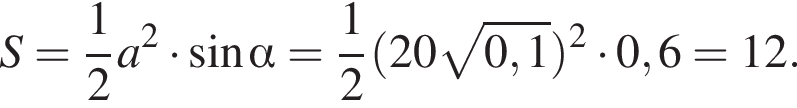
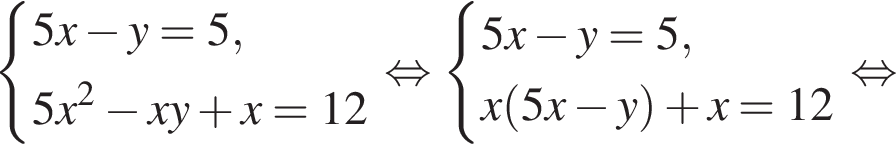
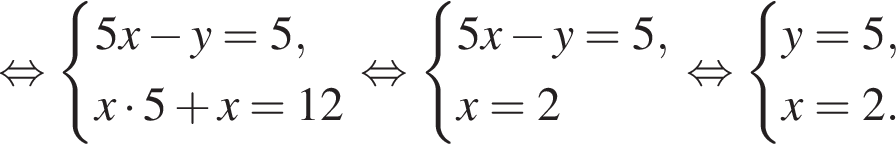
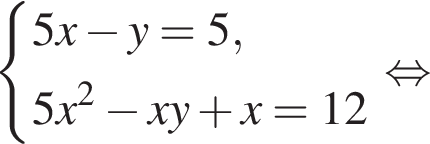
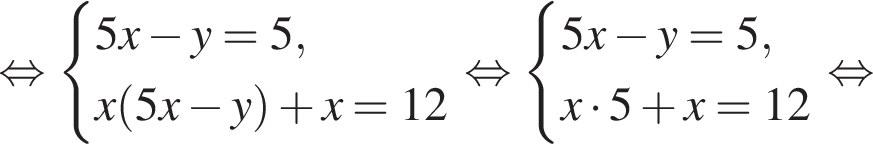
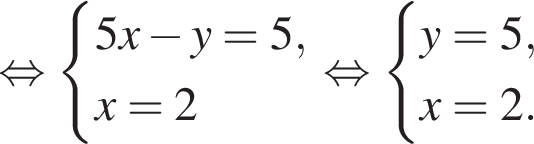
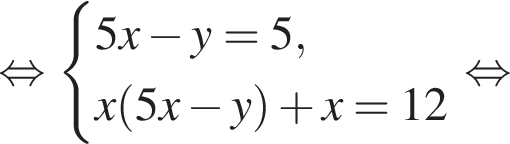
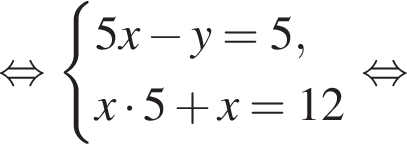
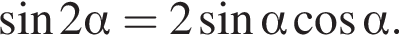 Тогда:
Тогда: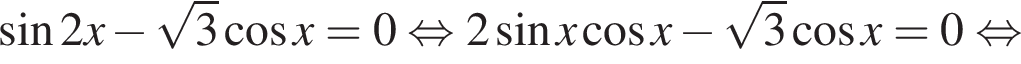
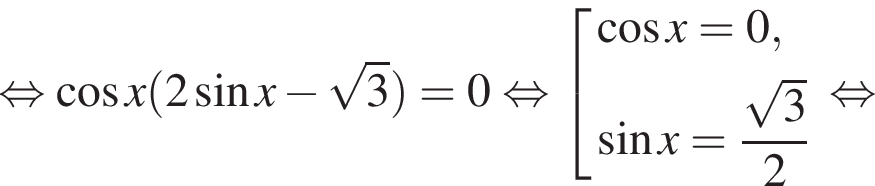
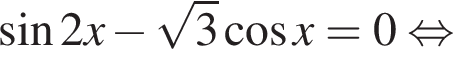
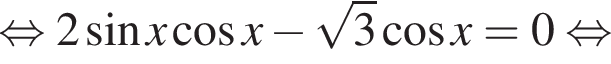
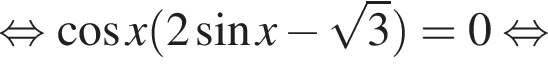
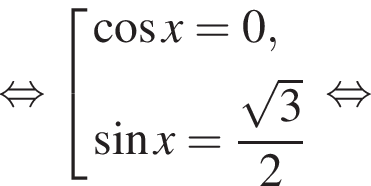
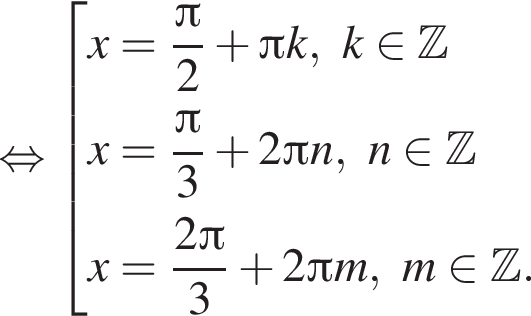
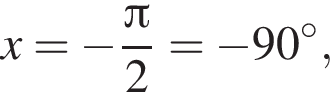 наименьшим положительным решением уравнения является корень
наименьшим положительным решением уравнения является корень 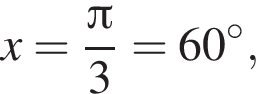 их сумма равна −30°.
их сумма равна −30°.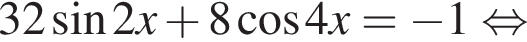
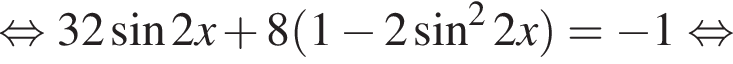
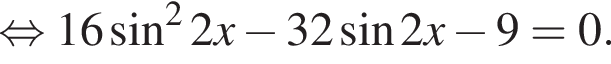
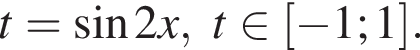 Тогда:
Тогда: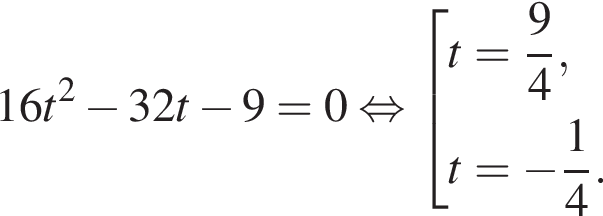
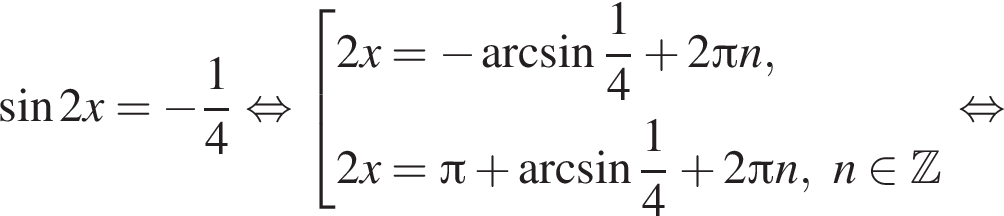
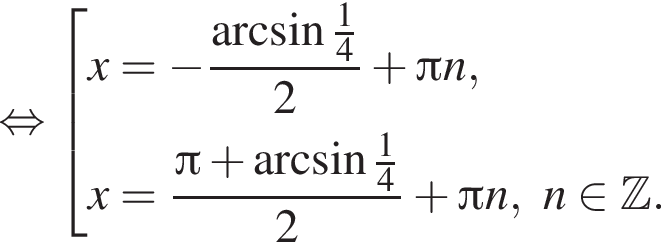
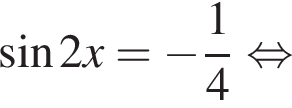
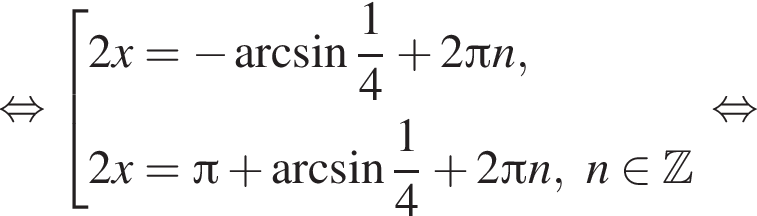
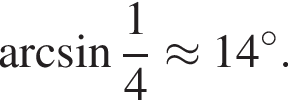 Рассмотрим значения x при различных значениях n:
Рассмотрим значения x при различных значениях n: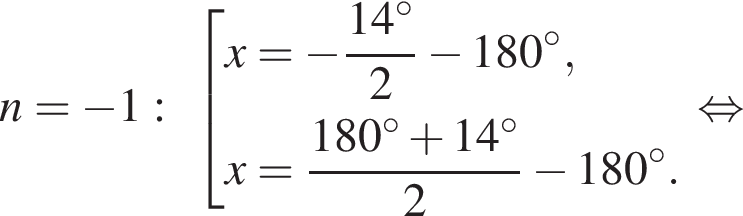
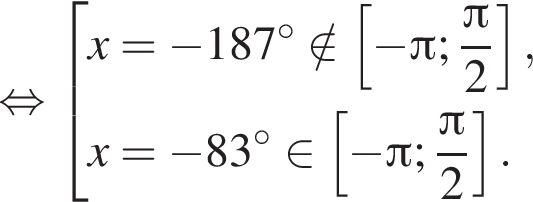

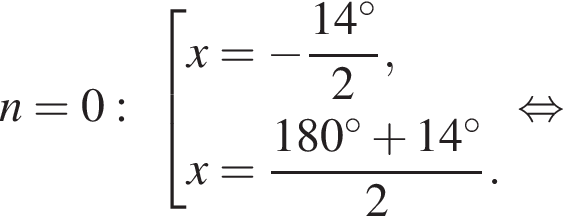
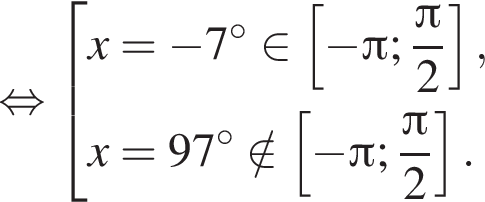
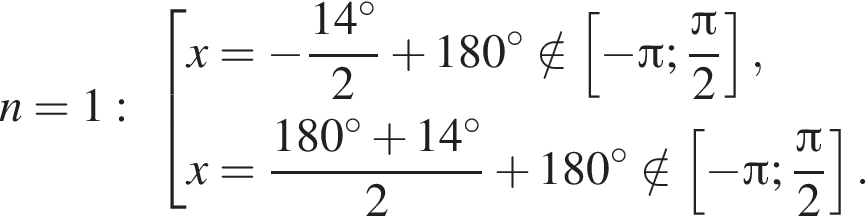
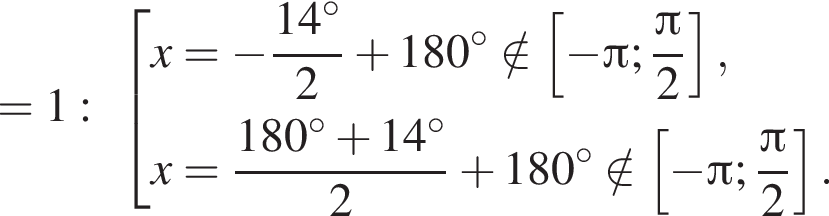
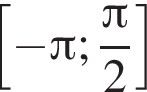 2 корня.
2 корня.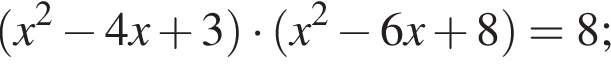
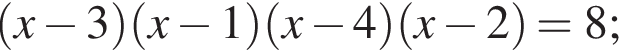
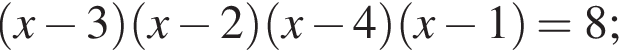
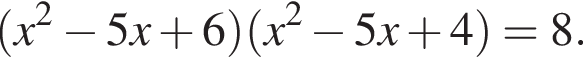
 Получим:
Получим: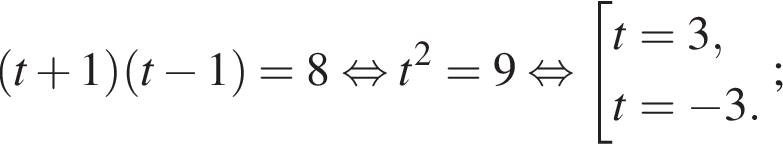
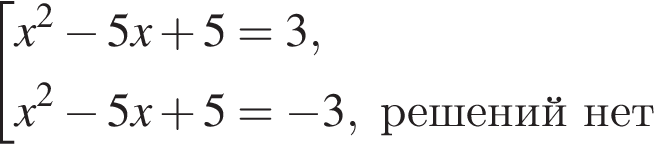
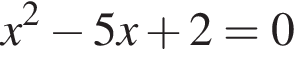 найдем по теореме Виета, она равна 5.
найдем по теореме Виета, она равна 5. искать ОДЗ не требуется.
искать ОДЗ не требуется.
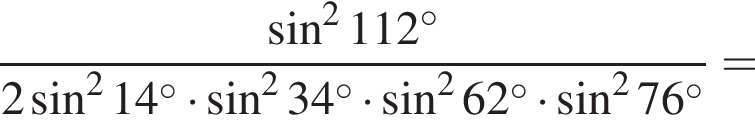
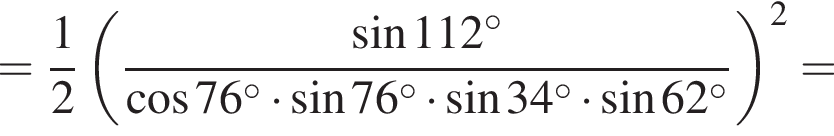
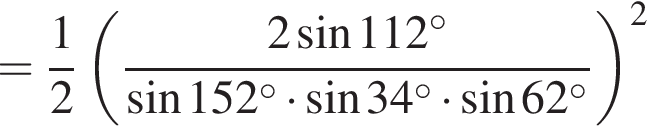
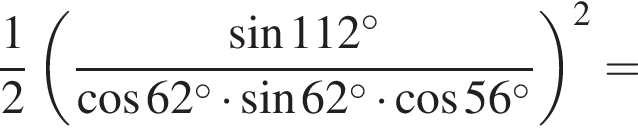
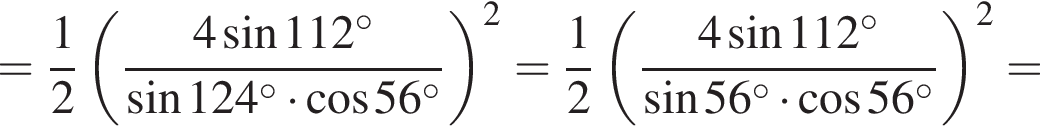
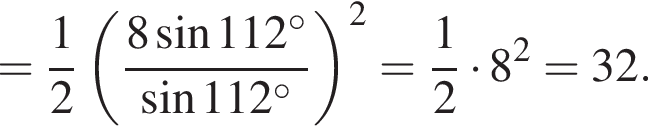
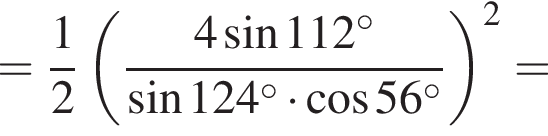
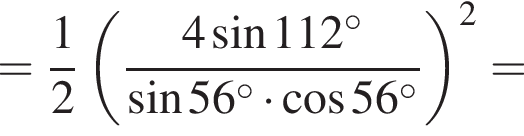
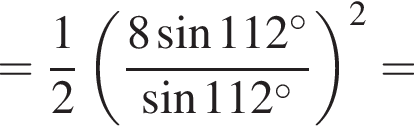
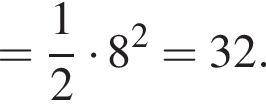
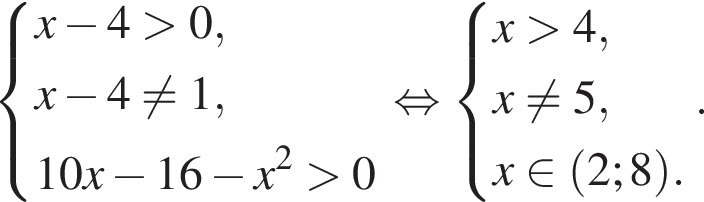
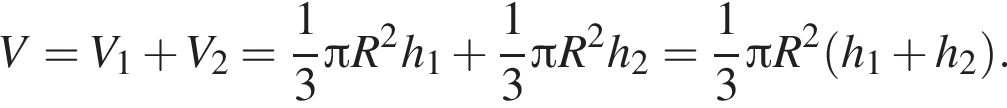
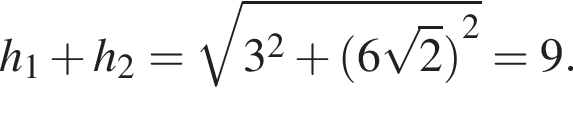 Высота, проведенная из прямого угла, является радиусом конусов и равна:
Высота, проведенная из прямого угла, является радиусом конусов и равна: 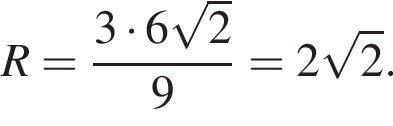 Поэтому:
Поэтому: 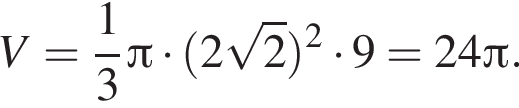
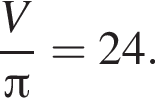
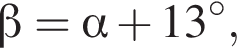 следовательно,
следовательно, 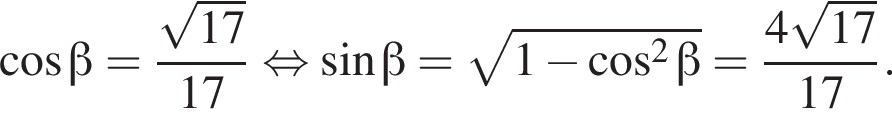
 Таким образом:
Таким образом: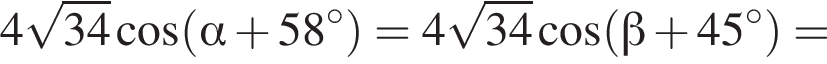
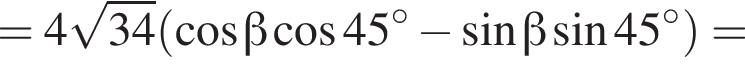
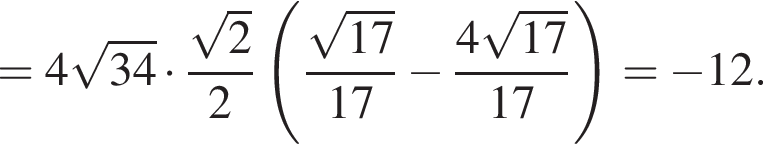
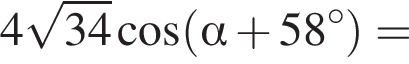
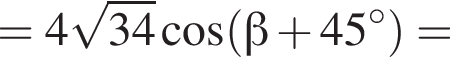

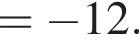
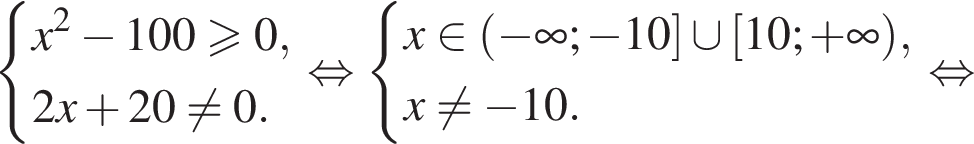
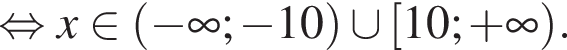
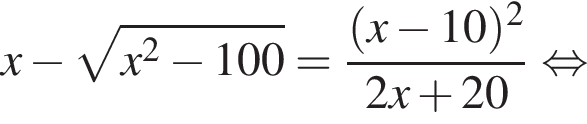
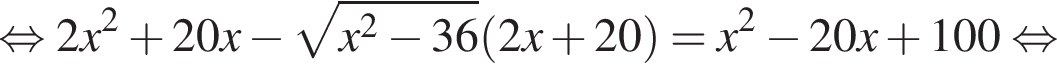
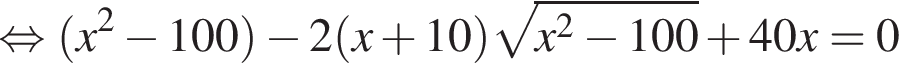
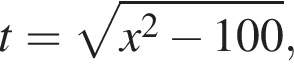 тогда
тогда 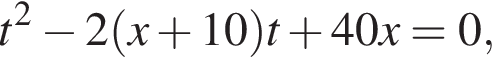 откуда
откуда 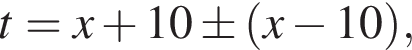 то есть
то есть